...space, Page 10, Almost there ... (gravitation)

6.4.6. Variable acceleration and comparison with inflation

If the mass-energy of the universe is assumed constant and given by m in Eq. (4), a continually decreasing universal acceleration is indicated, approaching but never reaching zero; this might be confirmed by measuring ever larger red shifts to note any variation in acceleration. Similarly, for r approaching zero, the acceleration approaches infinity, somewhat in accord with inflation scenarios but without the discontinuities. Thus, the horizon (causally disconnected regions), and flatness (fine tuned Hubble parameter producing near critical mass density) problems of the standard big bang model are addressed implicitly. See also Sect. 6.3.3.

Generally, given a constant mass m of the universe and depending on initial conditions, the solution to Eq. (4) indicates the size, velocity and acceleration of the universe at any time. More concretely, this equation may be applied to any segment of space, such as to the local supercluster (Sect. 2), where the mass is known, along with size, velocity and acceleration so that the relation may be run backward to the big bang or forward to the future for this region, and similarly for any observable or projected region.

6.4.7. Identity rather than equivalence of inertial and gravitational mass

Should experiment with greater precision indicate a difference between inertial and gravitational mass, the present thesis would be weakened (see Sect. 6.3). "Equivalence" is not as certain as "identity" here in that any coincidental equivalence may be under restricted conditions.

6.4.8. The indistinguishability among particles of the same kind

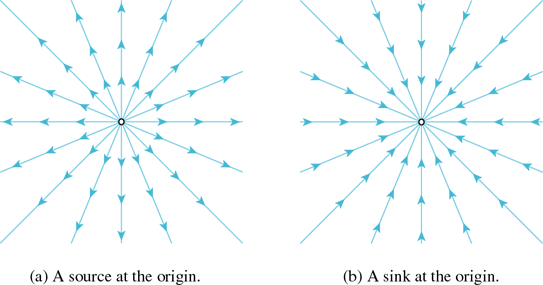
If elementary particles are gravitational sources, as is the general convention, rather than gravitational sinks as presently viewed, it would be possible to distinguish one particle from another (a newly created from a primitive) of the same kind, which contradicts convention (see Sect. 6.3.4). (continued above)

A L M O S T T H E R E . . .